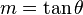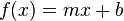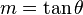imagenes de funciones

Funciones crecientes, decrecientes y constantes

Definición:  Sea I in intervalo en el dominio de una función f.  Entonces:

1) f es creciente en el intervalo I si f(b)>f(a) siempre que b>a en I.

2) f es decreciente en el intervalo I si f(b)<f(a) siempre b<a en I.

3) f es constante en el intervalo I si f(b) = f(a) para todo a y b en I.

Ejemplos:

1) 

Ejemplos de funciones  y de ecuaciones :

La siguiente gráfica define una función, línea recta con pendiente (m = 1) que pasa por el origen, la cual es función debido a no existe un elemento del dominio que relaciones dos elementos del codominio. El dominio es (-¥, ¥) o lo que equivale a decir que el dominio toma todos los valores sobre la línea recta. El rango de la función o codominio es también el mismo,  ya que toma todos los valores en el eje de las Y´s (-¥, ¥).

 

 La expresión mediante la cual puede representarse esta ecuación es la siguiente:

 

Y(x)= x   (otra forma de expresar este resultado también es la expresión f(x)=x)
Gráfica
                        

Esta ecuación no tiene asociado dos elementos del codominio con uno del dominio, sin embargo la definición de función no impone ninguna restricción al respecto.

 

Podemos analizar que en este caso el domino es (-¥, ¥). Sin embargo, sabemos que el hecho de que la función sea f(x)=x²  conduce a  que solo el recorrido de la función mande a valores positivos, y por tanto el rango de la función es [0, ¥)

                      

La siguiente ecuación  y² = x
 

Su gráfico es el siguiente:

                             

funcion de la forma y=mx+b

En matemática, el término función lineal puede referirse a dos conceptos diferentes.
En el primero, correspondiente a la geometría y el álgebra elemental, una función lineal es una función polinómica de primer grado. Es decir, una función que se representa en el plano cartesiano como una línea recta.
Esta función se puede escribir como

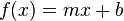
Una función lineal de una única variable dependiente x suele escribirse en la forma siguiente

que se conoce como ecuacion de la recta en el plano xy.
En la figura se ven dos rectas, que corresponden a las ecuaciones lineales siguientes:

en esta recta el parámetro m= 1/2, esto es el crecimiento de la recta es 1/2, cuando aumentamos x en una unidad, y aumenta en 1/2 unidad, el valor de b es 2, luego la recta corta el eje y en el punto y= 2
La ecuación:

la pendiente de la recta, el parámetro m= -1, indica que cuando el valor de x aumenta en una unidad, el valor de y disminuye en una unidades, el corte con el eje y, lo tiene en y= 5, dado que el valor de b= 5.
En el caso de una recta el valor de m se corresponde al ángulo de inclinación de la recta con el eje de las x a través de la expresión:

proposito

Como resultado del estudio de este bloque temático

se espera que los alumnos:

1.Transformen expresiones algebraicas en

otras equivalentes al efectuar cálculos.

2.Apliquen los criterios de congruencia de

triángulos en la justificación de propiedades

de figuras geométricas.

3.Resuelvan problemas que implican relacionar

ángulos inscritos y centrales de una

circunferencia.

4.Resuelvan problemas que implican deter

una razón de cambio, expresarla algebraicamente

y representarla gráfica

minarmente.